Modelling extinction events

Starting from the ODE model presented by Frank et. al. in “Investigating Anthropogenic Mammoth Extinction with Mathematical Models”, and discussed in previous posts, we include spatial variation by extending the model into a continuum. We remark that the equations have already been non-dimensionalised.

Now, \( H(x,t)\) and \(M(x,t)\) denote human and mammoth densities, and not the total number of individuals. By using a conservation of mass argument and integrating over an aribitrary domain and using the divergence theorem, we can derive a PDE system

Here, the fluxes \(\boldsymbol{J}\) represent the density of each species leaving a point of the domain. We must relate the flux to the densities and their spatial derivatives. Assuming mammoths try to distribute themsleves uniformly to maximise grazing grounds and minimise intraspecies conflict, we can postulate a simple consitute law akin to Fourier’s law for heat flux,

so that mammoths migrate from areas of high density to areas of low density (and their movements are not directly influenced by what humans are doing). Although we could assume a similar law for humans, we will build a “tracking” term into the flux. In particular, we want humans to go from areas of low mammoth density to areas of high mammoth density, at a rate proportional to the number of humans in that location, so that a simple flux for our movement can be given by

This choice for the flux makes the flux nonlinear, and the fact that we do not care about the gradient of human population density makes this term slighlty atypical. As the PDEs where already nonlinear this is not that much of a sacrifise.

We now need to decice on the boundary conditions. Periodic boundary conditions usually allow for nice spectral methods, but continents are not periodic, so in the sake of realism we go for Neumann (no flux) boundary conditions on the edges of the domain. This means \(\boldsymbol{n}\cdot\boldsymbol{\nabla}H,M=0\) with n the unit outward normal to the domain. If we had a powerful enough computer, we could discretise the continental United States, compute the unit normal at each element and solve the equations in that domain. Unfortunately we do not have a supercomputer and we just stick to the 1D case for now.

We now must choose how to discretise the domain. The method of lines (discretising space and leaving a system of many time-dependent ODE problems) is already a good start, but the nonlienar growth, coupling and fluxes means we need to be really careful with the next step. Finite differences is likely to struggle, and finite elements and volumes are too engineery for the writer’s taste, so we try an spectral method. The FFT is not rescuing us here because of our boundary conditions, but the Discrete Cosine Transform might.

The DCT world is quite complicated (SciPy has like 4 different types, each with its own sign convention), so my recommendation is just picking one, type II in our case, and just sticking with it. Also, if you are unsure if your transform will work with the kind of solutions that will show up, a good check is to transform and inverse transform a candidate solution

Unlike in the ODE case, our investigation here is not so focused on wether mammoths go extinct or not, but we just want to see some cool solutions. Cool solutions in this field means a travelling wave: a front of humans advancing onto a mammoth population. We can see this in the spatio temporal diagrams below, where we see how a healthy population of mammoths goes extinct after the introduction of a small population of humans to the left of the domain. Here, red means healthy population and blue means extinction. Further to this, we can see how a front of humans (the yellow line) advances from the left side to the right side of the domain in about 2 time units (all variables are dimensionless), and we can also see the corresponding receeding front of mammoth population density.

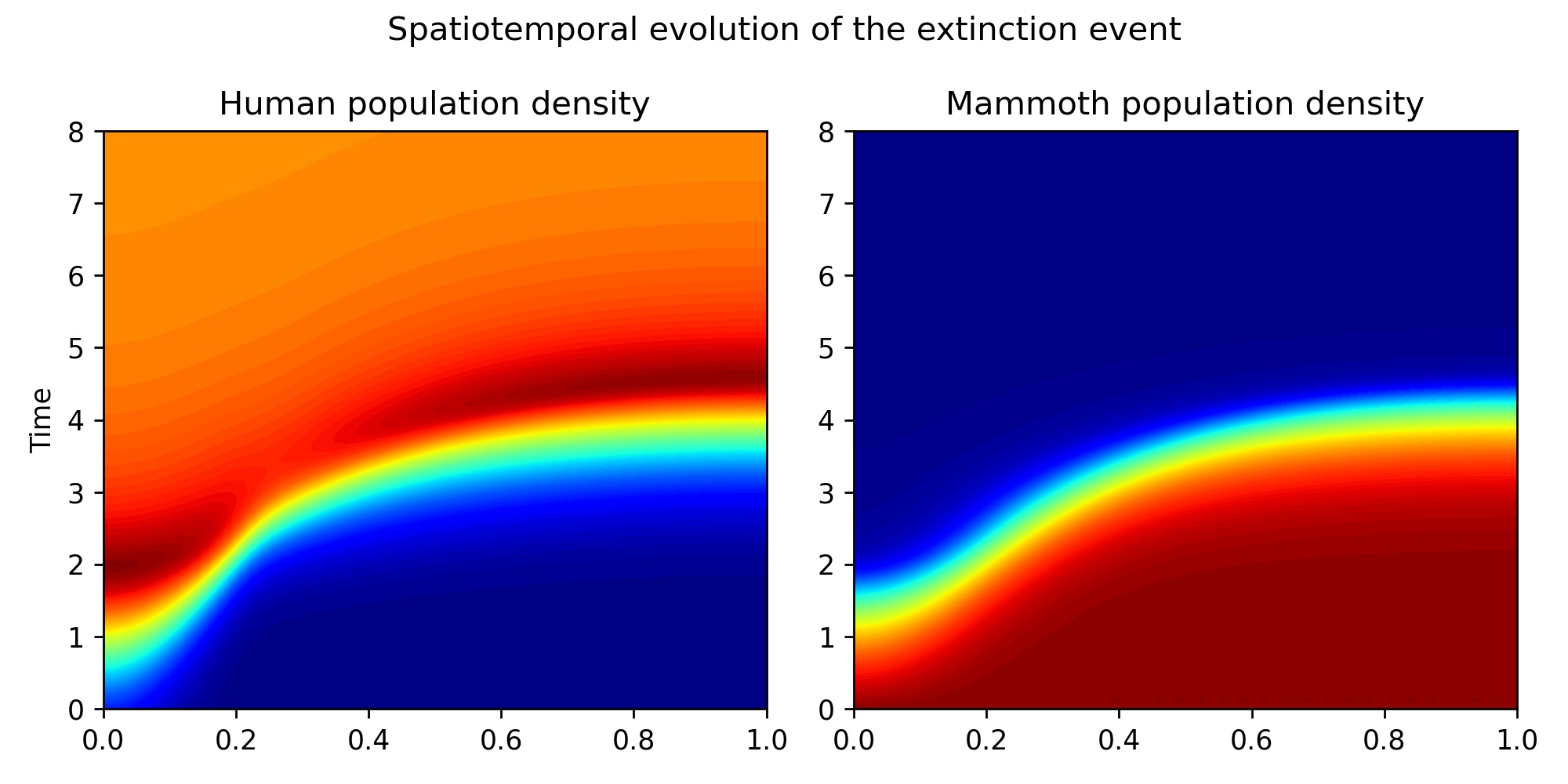
With this choice of parameters humans grow their numbers locally before moving on to the next location. We can see this more celarly by looking at a video of the evolution of the spatial distribution of both species.

from scipy.fft import dct, idct,dctn, idctn
import numpy as np
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt


def spectral_derivative(u, L):
    N = len(u)
    k = np.arange(N)
    return idctn((1j* k * np.pi / L * dctn(u, type=2, norm='ortho')), type=2, norm='ortho')

def RHS(t, y,  L, N, A_H, B_H, r,alpha, A_M,B_M,D):
    #N, L, A_H, B_H, r, B_M, alpha, D = params
    H, M = np.split(y, 2)
    
    # Compute spatial derivatives
    dHdx = spectral_derivative(H, L)
    dMdx = spectral_derivative(M, L)
    d2Hdx2 = spectral_derivative(dHdx, L).real
    d2Mdx2 = spectral_derivative(dMdx, L).real
    
    # Compute div(H grad(M))
    div_H_grad_M = spectral_derivative(H * dMdx, L).real
    
    # Compute right-hand sides
    dHdt =  A_H * H*(1-H) + M**2*H/(M**2+r**2) * B_H - D * div_H_grad_M #+ d2Hdx2
    dMdt =  A_M * M*(1-M)*(M*alpha - 1) - M**2*H/(M**2+r**2) * B_M + D * d2Mdx2
    
    return np.concatenate([dHdt, dMdt])

L = 1  # Length of the interval
N = 64   # Number of spatial points
T = 8 # Total simulation time
Nt = 200
dt = T/Nt # Time step for output

# Set up the grid
x = np.linspace(0, L, N, endpoint=True)

# Set up the initial conditions (example)
H0 = 0.2*np.exp(-(x)**2/0.01)
M0 = 1 + 0.1 * np.cos(2 * np.pi * x / L)*0

# Combine initial conditions into a single vector
y0 = np.concatenate([H0, M0])

# Set up the parameters for the PDEs
params = {
    'A_H': 1.0, 'B_H': 1, 'A_M': 0.1, 'B_M': 1,
    'D':0.01,'r':0.1,'alpha':10
}
t_span = (0, T)  # From t=0 to t=10
t_eval = np.linspace(0, T, Nt)
# Solve the PDE system
sol = solve_ivp(
    lambda t, y: RHS(t, y, L, N, **params),
    [0, T],
    y0,
    t_eval = t_eval,
    method='LSODA'
)

# Extract solution
H_sol = sol.y[:N]
M_sol = sol.y[N:]